Новый метод синтеза множеств точек многомерного пространства с малым отклонением
Калугин А.Н., Калугин Н.А.

Институт систем обработки изображений РАН,
Самарский государственный аэрокосмический университет имени академика С.П. Королёва
(национальный исследовательский университет) (СГАУ)

Аннотация:
Современные подходы к решению задач фотореалистического синтеза изображений основаны на использовании методов квази-Монте Карло. Эффективность этих методов зависит от свойств множества точек многомерного пространства. Существующие методы синтеза множеств точек многомерного пространства с малым отклонением позволяют генерировать множества, величина звездного отклонения которых увеличивается с ростом размерности генерируемого множества. В работе предлагается новый метод синтеза множеств точек многомерного пространства, основанный на использовании канонических систем счисления. Показывается, что предложенный метод позволяет в определенном смысле преодолеть так называемое «проклятие размерности».

Ключевые слова:
множества с малым отклонением, канонические системы счисления, звёздные отклонения.

Литература:

Ермаков, С. М. Метод Монте-Карло и смежные вопросы / С.М. Ермаков. - М., 1971.
Соболь, И. М. Численные методы Монте-Карло / И.М. Соболь - М., 1973.
Metropolis, N., Ulam, S. The Monte Carlo Method, J. Amer. statistical assoc. 1949 44 № 247 335—341.
Кнут, Д. Получисленные алгоритмы / Д. Кнут. - Искусство программирования. Том 2. Получисленные методы = The Art of Computer Programming, vol.2. Seminumerical Algorithms. — 3-е изд. — М.: «Вильямс», 2007. – С. 832.
Rubinstein, R.Y. Simulation and the Monte Carlo Method (second edition) / R. Y. Rubinstein, D.P. Kroese. - New York: John Wiley & Sons, 2007.
Niederreiter, H. Random Number Generation and Quasi-Monte Carlo Methods / H. Niederreiter. - SIAM, Philadelphia, 1992.
Tezuka, Sh. Financial Applications of Monte Carlo and Quasi-Monte Carlo methods / Shu Tezuka // Random and Quasi-Random Point Sets, P. Hellekalek, G. Larcher, Eds, Lecture notes in statistics, 138. - Springer, 1998.
Keller, A. Myths of Computer Graphics / A. Keller // H. Niederreiter and D. Talay, eds. Monte Carlo and Quasi-Monte Carlo Methods 2004, pp. 217-243. - Springer, 2006.
Drmota, D. Sequences, Discrepancies and Applications / D. Drmota, R. F. Tichy // Lecture Notes in Mathematics, vol 1651. - Berlin: Springer, 1998.
Faure, H. Discrepancy and diaphony of digital (0,1)-sequences in prime base/ H. Faure // Acta Arith, 117, pp. 125–148, 2005.
Ninomiya, S. Constructing a new class of low-discrepancy sequences by using the 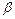-adic transformation/ S. Ninomiya // Mathematics and Computers in Simulation, Vol. 47, 2, pp. 403 – 418. – Elsevier, 1998.
Кейперс, Л. Равномерное распределение последовательностей: / Л. Кейперс, Г. Нидеррейтер пер. с англ., под ред. С.М. Ермакова. – М.: Наука, Гл. ред. физ.-мат. Лит., 1985 – 408 с.
Random and Quasi-Random Point Sets / P. Hellekalek, G. Larcher, Eds // Lecture notes in statistics, 138. - Springer, 1998.
Kátai, I. Canonical number systems in imaginary quadratic fields / I. Kátai, B. Kovács // Acta Mathematica Academiae Scientarium Hungaricae. 37 (1-3), 1981, pp. 159-164.
Kátai, I. Generalized Number Systems in Euclidean Spaces / I. Kátai // Mathematical and Computer Modeling, 38, 2003, pp. 883-892.
Kovács, A. Generalized binary number systems / A. Kovács // Annales Univ. Sci. Budapest, Sect. Comp. 20, 2001, pp. 195-206.
Kovács, A. On number expansions in lattices / A. Kovács // Proc. 5th Internation Conference on Applied Informatics. - Eger, Hungary, 2001.
Kovács, B. Canonical number systems in algebraic number fields / B. Kovács // Acta Math. Acad. Sci. Hungar., 37 (1981), pp. 405-407.
Akiyama, S. New criteria for canonical number systems / S. Akiyama, H. Rao// Acta Arithm., 111 (2004), pp. 5—25.
Kovács, B. Canonical number systems in algebraic number fields / B. Kovács // Acta Math. Acad. Sci. Hungar., 37 (1981), 405-407.
Калугин А.Н., Генератор LSFR-CNS: аналитическое исследование равномерности распределения / А.Н. Калугин // Компьютерная оптика. В. 31. – Самара, Институт систем обработки изображений РАН, 2007.
Калугин, А.Н. Разработка и исследование многомерных генераторов равномерно распределенных псевдослучайных векторов, основанных на представлении данных в алгебраических полях / А.Н. Калугин. Диссертация на соискание ученой степени кандидата физико-математических наук. Рукопись.
Chernov, V.M. Fast uniform distribution of sequences for fractal sets / V. M. Chernov // Proceedings of International Conference on Computer Vision and Graphics, 2004, September 22-24, 2004, Warsaw, Poland, Computational IMAGING AND VISION SERIES. - Kluwer Academic Press.